II. Théorie des champs
Le groupe de renormalisation fonctionnel (FRG) est un outil théorique puissant pour l’étude des systèmes fortement corrélé et des phénomènes critiques. Il permet de décrire de manière non perturbative les fluctuations présentes à toutes les échelles, particulièrement dans les systèmes où les méthodes traditionnelles échouent. L'approche par le FRG est particulièrement adaptée à l'étude des transitions de phase de second ordre, ainsi des aux systèmes en basses dimensions, où les fluctuations quantiques et thermiques jouent un rôle essentiel.
Chercheurs : Adam Rançon, Alexandre Feller
Applications dans les gaz d'atomes froids
Les gaz d’atomes froids, notamment dans des systèmes de basse dimension, sont des plateformes idéales pour explorer des phénomènes quantiques fondamentaux. Par exemple, le FRG a été utilisé pour étudier la thermodynamique des gaz de Bose en deux dimensions (2D). Ces systèmes sont particulièrement difficiles à décrire en raison de la présence de fortes fluctuations de phase et de défauts topologiques tels que les vortex. Il a été montré que le FRG permet de décrire avec précision la thermodynamique universelle des gaz de Bose bidimensonnels, ainsi qu'une quantité clé dans ces gaz, le contact de Tan, qui relie les corrélations à courte portée entre atomes et la thermodynamique du gaz. L’approche FRG a ainsi pu capturer avec précision les comportements observés près de la transition superfluide (transition de Kosterlitz-Thouless), en fournissant une excellente concordance avec les résultats expérimentaux. [Phys. Rev. A 85, 063607 (2012), Phys. Rev. Lett. 129, 263401 (2023)]
Généralisation du Théorème Centrale Limite près de points critique
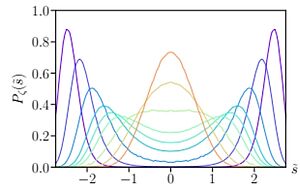
La distribution de probabilité du paramètre d'ordre près d'une transition de phase est un outil clé pour caractériser les comportements critiques dans les systèmes physiques. En théorie des champs, cette distribution permet de décrire les fluctuations qui accompagnent une transition de phase du second ordre, révélant des propriétés universelles du système. Contrairement à la prédiction classique du théorème central limite, où la somme de variables aléatoires devient gaussienne, les systèmes fortement corrélés à proximité des points critiques affichent des distributions non-gaussiennes. Grâce au FRg, il a été possible de calculer ces distributions universelles de manière précise. Le FRG permet de relier la somme de variables corrélées à une généralisation du théorème central limite, décrivant ainsi des comportements non-triviaux qui échappent aux approches traditionnelles. Ces résultats apportent une compréhension plus profonde de la dynamique des systèmes critiques et permettent de relier les propriétés microscopiques à la physique macroscopique dans un cadre universel. Phys. Rev. Lett. 129, 210602 (2022)
