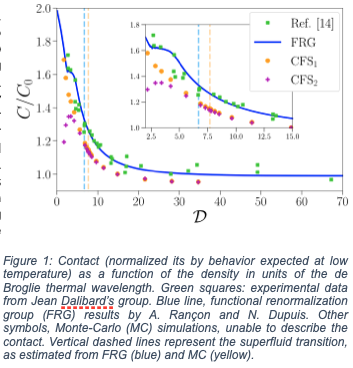
In low-dimensional systems like 2D systems, quantum and thermal fluctuations are strong, making it challenging to use standard methods to describe their physics. An example is ultracold 2D Bose gases, which pose challenges due to strong phase fluctuations and the presence of vortices. Recently, experiments at Collège de France, led by Jean Dalibard's team, measured the Tan's contact of a 2D Bose gas. This quantity is interesting as it describes short-range correlations between cold atoms and is related to thermodynamics. Traditional methods like Monte-Carlo simulations struggled to describe the contact's behavior with temperature, especially in the highly fluctuating regime and at the superfluid transition (the Kosterlitz-Thouless transition). Using the functional renormalization group, we demonstrated the method's ability to fully describe the contact in all regimes (see Figure 1). This research was published in Phys. Rev. Lett. 129, 263401 (2023).

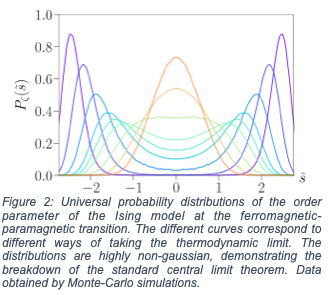
Second-order phase transitions involve a gradual change in a system's properties with a varying control parameter like temperature. These transitions exhibit universal critical behavior, meaning their behavior near the critical point doesn't depend on microscopic details. This is due to long-range correlations, not microscopic specifics. The central limit theorem (CLT) states that the sum of many independent, identically distributed random variables will be Gaussian. However, near second-order phase transitions where components are strongly correlated, the standard CLT doesn't apply. Using the functional renormalization group,  we've developed a way to describe the behavior of strongly correlated variables (like spins), akin to a generalized CLT. These distributions are universal but not Gaussian (see Figure 2), as detailed in our publication  Phys. Rev. Lett. 129, 2106102 (2022).