Soliton gases in Optics and in Hydrodynamics (SOGOOD ANR Project)

Soliton gas (SG) is a concept in statistical mechanics and nonlinear physics that has been originally introduced by V. Zakharov as a large random ensemble of interacting solitons in integrable equations such as the nonlinear Schrodinger equation that can be solved using  the inverse scattering transform (IST) method. The overall objective of the SOGOOD ANR project (2022-2026) is to build an interdisciplinary experimental and numerical approach combining optics and hydrodynamics to investigate the dynamical, statistical and thermodynamic properties of SGs as well as the robustness of this concept relatively to the perturbations to integrability of the wave system. Our experimental platforms are 1D and 2D water tanks available at LEGI (Université de Grenoble-Alpes), LHEEA (Ecole Centrale de Nantes), MSC (Université Paris Cité) together with recirculating fiber loops and time-lens systems (PhLAM).

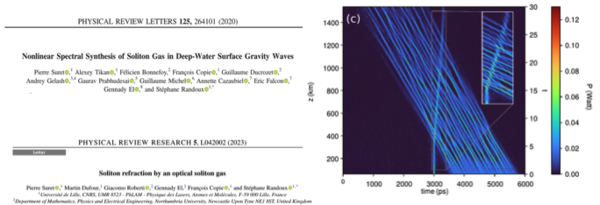
In recent experiments, we have reported the controlled synthesis of a dense soliton gas in deep-water surface gravity waves using the tools of nonlinear spectral theory (IST method) [https://doi.org/10.1103/PhysRevLett.125.264101]. We have evidenced a refraction phenomenon where a tracer soliton experiences an effective velocity change due to its interaction with an optical soliton gas. This effective velocity change has been found to be in good quantitative agreement with the results of the spectral kinetic theory of soliton gas [https://doi.org/10.1103/PhysRevResearch.5.L042002].