I. Condensat de Bose-Einstein

Les transitions de phase sont omniprésentes en physique, englobant des phénomènes thermiques comme l'ébullition de l'eau jusqu'aux transitions magnétiques dans les solides. Elles comprennent des transitions cosmologiques dans l'univers primordial et la transition vers un plasma quark-gluon lors de collisions à haute énergie.

Les transitions de phase quantiques, particulièrement intrigantes, se produisent à des températures proches du zéro absolu et sont provoquées par des fluctuations quantiques plutôt que thermiques. L'intensité des fluctuations est très sensible à la dimensionnalité des systèmes physiques, ce qui détermine l'existence et la nature des transitions de phase. Les systèmes de faible dimension présentent souvent une suppression des transitions de phase, tandis que les systèmes de haute dimension tendent à montrer un comportement de type champ moyen. La transition d'Anderson de localisation-délocalisation se distingue parmi les transitions de phase quantiques, car elle conserverait son caractère non champ moyen dans toutes les dimensions.

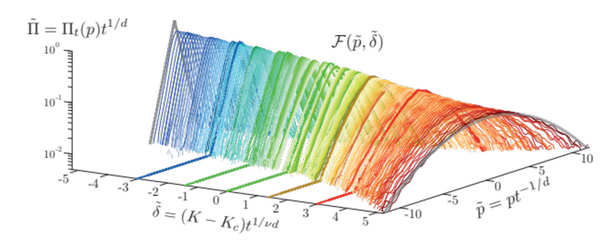
Des expériences récentes marquent la toute première observation et caractérisation de la transition d'Anderson en quatre dimensions, en utilisant des atomes ultra-froids comme simulateurs quantiques avec des dimensions synthétiques. Nous caractérisons la dynamique universelle à proximité de la transition de phase. Nous mesurons les exposants critiques décrivant les propriétés d'invariance d'échelle de la dynamique critique, qui obéissent à la loi d'échelle de Wegner. Notre travail constitue la première démonstration expérimentale que la transition d'Anderson n'est pas de type champ moyen en dimension quatre.

Cette thématique phare de l’équipe Gaz Quantiques est fruit de collaborations de longue date avec des chercheurs du LKB Paris (Dominique Delande, Nicolas Cherroret) et NUS Singapour (G. Lemarié).

Voir aussi :

• Exploration de la criticité d’une transition de phase quantique en 4D : arXiv:2402.06573

• Etude de la forme de la distribution asymptotique localisée : Eur. Phys. J. D 76 103 (2022)

• Réalisation d'un système désordonné de Floquet idéal : New J. Phys. 21 035008 (2019)

• Fonction d’échelle de la localisation d’Anderson 2D : PRL 115 240603 (2015)

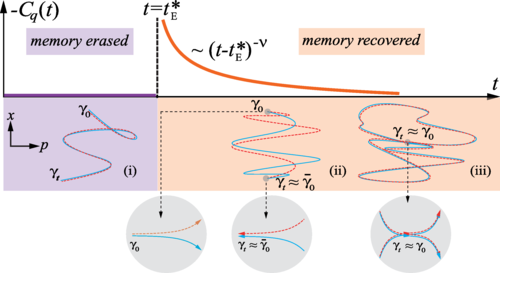
Le chaos quantique, caractérisé par le comportement des systèmes quantiques dont les limites classiques sont chaotiques, ne conduit pas toujours à une sensibilité aux conditions initiales. Dans certaines conditions, ces systèmes peuvent subir une transition de phase dynamique, modifiant soudainement leur comportement vis-à-vis de la mémoire des conditions initiales. Avant un certain temps critique t_E, le système est chaotique et ne conserve pas cette mémoire ; après ce temps, l’interférence quantique augmente la probabilité de retour à l’état initial. Le temps t_E est lié à la notion de ‘temps d’Ehrenfest’ τ_E, correspondant à la transition classique-quantique du système. Utilisant une expérience de rotateur frappé atomique avec des atomes de Cs refroidis par laser, nous avons observé un changement soudain du comportement du système, acoquinée a cette transition : avant le temps critique, le système subit un mouvement chaotique dans l'espace des phases et sa mémoire des états initiaux est effacée ; après le temps critique, l’interférence quantique augmente la probabilité qu'une trajectoire chaotique revienne à l'état initial, permettant ainsi au système de récupérer sa mémoire initiale [PRL 121 134101 (2018)].

Ces résultats sont issus d’une collaboration théorique avec Chushun Tian, chercheur à l'Académie chinoise des sciences.

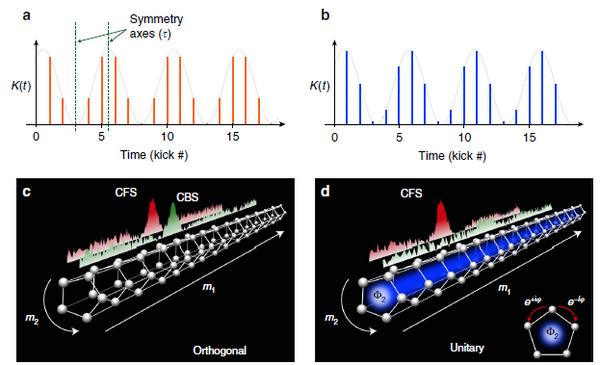
Les propriétés de localisation des systèmes désordonnés sont sensibles à leurs caractéristiques de symétrie de l’Hamiltonien. Cependant, cette question a été peu explorée expérimentalement jusqu'à présent. Grâce à un contrôle temporel précis des modulations de potentiel, nous avons démontré la réalisation d'un champ de jauge artificiel dans une dimension synthétique (temporelle) d'un système quantique désordonné excité périodiquement (de Floquet). En ajustant la force de ce champ de jauge, nous pouvons contrôler les propriétés de symétrie de renversement temporel du système, que nous sondons à travers l'observation expérimentale de trois signatures révélatrices et sensibles à la symétrie de la localisation. Les deux premières sont la rétrodiffusion cohérente (so-called « coherent backscattering », CBS) [PRL 118 184101 (2017)], marqueur de la localisation faible, et la diffusion cohérente vers l'avant (« coherent forward scattering », CFS), véritable signature d'interférence de la localisation d'Anderson, que nous avons observée expérimentalement pour la première fois [Nat. Commun. 9 1382 (2018)]. La troisième est la mesure directe de la fonction d'échelle β(g) dans deux classes de symétrie différentes, permettant de démontrer son universalité ainsi que l'hypothèse de l'échelle à un paramètre. [PRA 97 061601 (2018)]