I. Bose-Einsten condensate
The Quantum Systems team recently developed the first Bose-Einstein Condensate (BEC) experiment at PhLAM. The BEC experiment uses potassium atoms with tunable interactions, and its ultimate goal is to explore new disorder and localization phenomena, related to the well-known many-body localization and quantum thermalization problems.
Researchers: Radu Chicireanu, Adam Rançon
PhD candidates: Charbel Cherfan (2018-2021), Maxime Denis (2019-2022), Farid Madani (2021-2024)
Post-docts: Isam Manai (2019-2020)
Experiment
The BEC device is distinguished by its extensive use of fiber optic amplifier technology (used in the telecommunications industry) throughout the entire experiment, opening the door to potential new applications for compact and transportable ultracold atom devices. Our original setup includes:
- A frequency stabilization scheme based on saturated absorption spectroscopy of acetylene, which, combined with a phase-shifting phase-locking scheme, can virtually cover the entire telecommunications C-band (1530-1565 nm) Optics Express 28, 494 (2020).
-
A high-power multi-frequency near-infrared laser system (achieved via second harmonic generation), capable of addressing D2 (767 nm) or D1 (770 nm) transitions, used for laser cooling of potassium atoms. Appl. Phys. Lett. 119, 204001 (2021).
-
A fiber-optic laser system for optical dipole trapping and condensation of potassium atoms. In a novel design, we are able to dynamically control laser power with a dynamic range of more than 40 dB and an extinction greater than 60 dB, without using free-space acousto-optic modulators, thus avoiding unnecessary optical losses and unwanted thermal effects (paper in preparation).
-
A pulsed laser system, based on a telecommunication pulsed fiber amplifier and second harmonic generation, to periodically drive the potassium BEC and realize a periodically driven dynamical system (struck rotator model) to study quantum chaos and localization phenomena (paper submitted early 2024 arXiv:2402.06573).

Disorder and localization in disordered quantum systems
Radu Chicireanu, Adam Rançon
Quantum simulations are a powerful tool for understanding complex quantum systems by using controlled and tunable experimental setups to mimic their behavior. A particularly intriguing application of quantum simulations is the study of Anderson localization, a phenomenon in which waves, whether quantum or classical, can become localized due to subtle interference effects, leading to the absence of scattering. This physics can be simulated quantumly using periodically time-modulated optical potentials (Floquet systems). In our case, we use a 1D optical lattice pulsed over time to excite a cloud of ultracold atoms and realize the famous "Kicked Rotor" model (or "rotator frape") as a paradigm of quantum chaos. Despite the relative simplicity of the system, this allows for the study of a very rich physics, ranging from quantum resonance phenomena and the creation of artificial gauge fields, to the study of Anderson localization and associated metal-insulator phase transitions. The paragraphs below present some recent significant results.
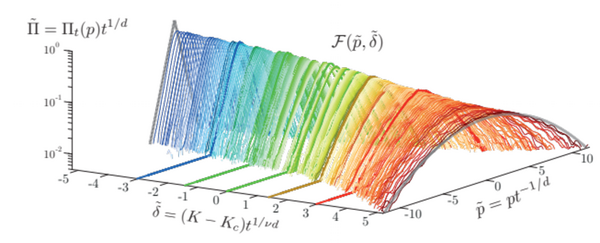
Anderson Transitions in Synthetic Dimensions
Phase transitions are ubiquitous in physics, encompassing thermal phenomena such as the boiling of water to magnetic transitions in solids. They include cosmological transitions in the early universe and the transition to a quark-gluon plasma during high-energy collisions. Quantum phase transitions, particularly intriguing, occur at temperatures close to absolute zero and are driven by quantum rather than thermal fluctuations. The intensity of the fluctuations is highly sensitive to the dimensionality of physical systems, which determines the existence and nature of phase transitions. Low-dimensional systems often exhibit phase transition suppression, while high-dimensional systems tend to exhibit mean-field behavior. The Anderson localization-delocalization transition stands out among quantum phase transitions because it is thought to retain its non-mean-field character in all dimensions.
Recent experiments mark the first-ever observation and characterization of the Anderson transition in four dimensions, using ultracold atoms as quantum simulators with synthetic dimensions. We characterize the universal dynamics near the phase transition. We measure the critical exponents describing the scale-invariant properties of the critical dynamics, which obey Wegner's scaling law. Our work constitutes the first experimental demonstration that the Anderson transition is not of the mean-field type in four dimensions. This flagship research topic of the Quantum Gases team is the result of long-standing collaborations with researchers from LKB Paris (Dominique Delande, Nicolas Cherroret) and NUS Singapore (G. Lemarié).
See also:
-
Exploring the criticality of a 4D quantum phase transition: arXiv:2402.06573
-
Studying the shape of the localized asymptotic distribution: Eur. Phys. J. D 76 103 (2022)
-
Realization of an ideal disordered Floquet system: New J. Phys. 21 035008 (2019)
-
Scaling function of 2D Anderson localization: PRL 115 240603 (2015)
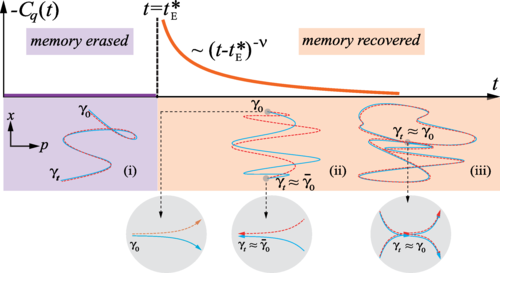
Classical-quantum transition and quantum chaos
Quantum chaos, characterized by the behavior of quantum systems whose classical limits are chaotic, does not always lead to sensitivity to initial conditions. Under certain conditions, these systems may undergo a dynamical phase transition, suddenly changing their behavior with respect to the memory of initial conditions. Before a certain critical time tE, the system is chaotic and does not retain this memory; after this time, quantum interference increases the probability of returning to the initial state. The time tE is related to the notion of ‘Ehrenfest time’ τE, corresponding to the classical-quantum transition of the system. Using an atomic hit rotator experiment with laser-cooled Cs atoms, we observed a sudden change in the system’s behavior, co-incident with this transition: before the critical time, the system undergoes a chaotic motion in phase space and its memory of initial states is erased; after the critical time, quantum interference increases the probability that a chaotic trajectory returns to the initial state, thus allowing the system to recover its initial memory [PRL 121 134101 (2018)].
These results come from a theoretical collaboration with Chushun Tian, a researcher at the Chinese Academy of Sciences.
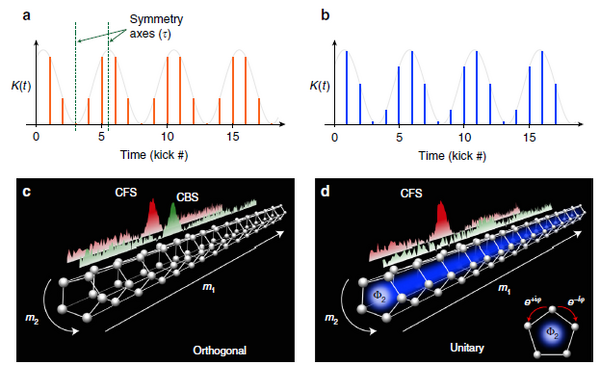
Symmetries in disordered quantum systems
The localization properties of disordered systems are sensitive to their Hamiltonian symmetry characteristics. However, this issue has been little explored experimentally so far. Through precise temporal control of potential modulations, we have demonstrated the realization of an artificial gauge field in a synthetic (time) dimension of a periodically excited disordered quantum (Floquet) system. By tuning the strength of this gauge field, we can control the time-reversal symmetry properties of the system, which we probe through the experimental observation of three telltale and symmetry-sensitive signatures of localization. The first two are coherent backscattering (CBS) [PRL 118 184101 (2017)], marker of weak localization, and coherent forward scattering (CFS), a true interference signature of Anderson localization, which we observed experimentally for the first time [Nat. Commun. 9 1382 (2018)]. The third is the direct measurement of the scaling function β(g) in two different symmetry classes, allowing to demonstrate its universality as well as the one-parameter scaling hypothesis. [PRA 97 061601 (2018)]
Localization Theory in Interacting Dynamic Systems
Adam Rançon, Radu Chicireanu
In connection with the new Bose-Einstein condensation experiment with controllable interactions, we have studied theoretically and numerically several scenarios on dynamical localization in the presence of interactions. In [PRA 101, 043624 (2020)], we analyzed the dynamics of a many-body atom rotor with mean-field interactions, governed by the Gross-Pitaevskii equation. We showed that the interaction destroys the dynamical localization, replacing it with subdiffusive behavior, without the subdiffusive exponent being universal.
Other studies have explored the effects of strong interactions of hard-core bosons in 1D, in the Tonks-Girardeau regime. In [PRA 104, 043302 (2021)], we demonstrated that dynamical localization persists, called Many-Body Dynamical Localization (MBDL), and that this phase is indeed thermal, in contrast to the ergodicity breaking observed in standard localized systems. The momentum distribution decays according to a power law at large moments, indicating a thermal Tan contact. Another study [Quantum 7, 917 (2023)] generalized these results to quasi-periodic modulations with three frequencies, realizing an effective Anderson localization/transition model in 3 dimensions. Similar to but not completely equivalent to the case without interactions, a Tonks gas subjected to a quasi-periodic potential shows a dynamical delocalization transition when the potential strength increases. Finally, we studied the Lieb-Liniger model in the few-body limit [PRA 103, 043314 (2021)], showing that two interacting bosons always localize dynamically, but their momentum distribution follows a C/k4 power-law decay, with a Tan C contact that remains finite at long times.
