II. Quantum field theory: UMR8523 - Laboratoire de Physique des Lasers, Atomes et Molécules

The functional renormalization group (FRG) is a powerful theoretical tool for studying strongly correlated systems and critical phenomena. It enables a non-perturbative description of fluctuations at all scales, particularly in systems where traditional methods fail. The FRG approach is especially well-suited for studying second-order phase transitions, as well as low-dimensional systems, where quantum and thermal fluctuations play an essential role.

Researchers: Adam Rançon

Applications in Cold Atom Gases

Cold atom gases, especially in low-dimensional systems, provide ideal platforms for exploring fundamental quantum phenomena. For example, the FRG has been used to study the thermodynamics of two-dimensional (2D) Bose gases. These systems are particularly challenging to describe due to the presence of strong phase fluctuations and topological defects such as vortices. It has been shown that the FRG can accurately describe the universal thermodynamics of 2D Bose gases, as well as a key quantity in these gases, Tan's contact, which links short-range correlations between atoms to the thermodynamics of the gas. The FRG approach has successfully captured the behaviors observed near the superfluid transition (Kosterlitz-Thouless transition), providing excellent agreement with experimental results. [Phys. Rev. A 85, 063607 (2012), Phys. Rev. Lett. 129, 263401 (2023)]

Generalization of the Central Limit Theorem near Critical Points

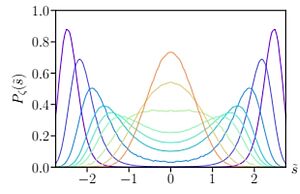
Universal probability distributions of the order parameter of the Ising model at the ferromagnetic-paramagnetic transition. The different curves correspond to different ways of taking the thermodynamic limit. The distributions are highly non-gaussian, demonstrating the breakdown of the standard central limit theorem. Data obtained by Monte-Carlo simulations.

The probability distribution of the order parameter near a phase transition is a key tool for characterizing critical behaviors in physical systems. In field theory, this distribution describes the fluctuations that accompany a second-order phase transition, revealing universal properties of the system. Contrary to the classical prediction of the central limit theorem, where the sum of random variables becomes Gaussian, strongly correlated systems near critical points exhibit non-Gaussian distributions. Thanks to the FRG, it has been possible to calculate these universal distributions with precision. The FRG allows for a connection between the sum of correlated variables and a generalization of the central limit theorem, describing non-trivial behaviors that elude traditional approaches. These results provide a deeper understanding of the dynamics of critical systems and allow the connection between microscopic properties and macroscopic physics within a universal framework.[Phys. Rev. Lett. 129, 210602 (2022)]