3) Solitons
Page en attente de traduction / Page awaiting translation
Bien que la première mise en évidence de solitons temporels dans les fibres optiques date de plus de 30 ans, cette thématique est toujours d’actualité au vu de leur fort potentiel pour la mise au point de sources à fibre compactes et ultra-courtes notamment. La manipulation des propriétés spectro-temporelles des solitons s’avère cependant assez délicate car elles dépendent du laser d’excitation, mais aussi des caractéristiques dispersives et non-linéaires des fibres optiques, qui correspondent aux paramètres de contrôle. Nous nous intéressons ici plus particulièrement au régime très court (< 100 fs) dans lequel l’effet Raman induit un auto-décalage spectral vers les hautes longueurs d’ondes.
a) Mise en évidence d’un nouveau mécanisme d’accumulation de solitons
Nous avons tout d’abord utilisé les fibres à bandes interdites photoniques (décrites plus en détail dans la partie intitulée « Modélisation de Fibres Avancées »), qui présentent des bandes de transmission discrètes, et une dépendance spectrale « exotique » de la dispersion et du coefficient non-linéaire. Plus particulièrement, ces deux grandeurs varient de façon brutale au voisinage des bords de bandes interdites photoniques. Nous avons alors montré théoriquement et expérimentalement que ces propriétés singulières permettent de stopper l’auto-décalage Raman de solitons, ce qui induit une accumulation de solitons à une longueur d’onde déterminée par la position du bord de bande interdite photonique [1]. Nous avons ensuite utilisé ce mécanisme pour proposer une nouvelle méthode passive de stabilisation de sources supercontinuum générées dans ce type de fibres [2].
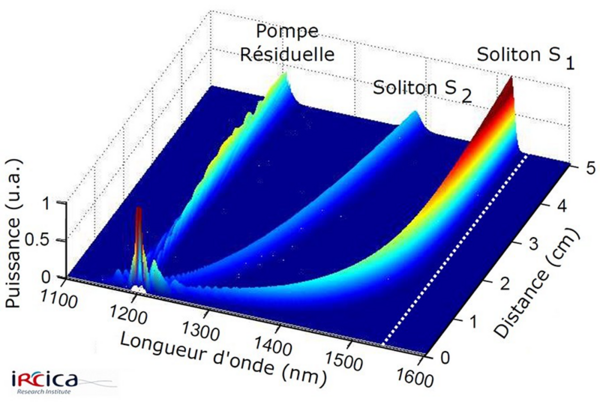
Résultat numérique : l’autodécalage Raman du premier soliton éjecté est fortement diminué à proximité du bord de bande (pointillés blancs).
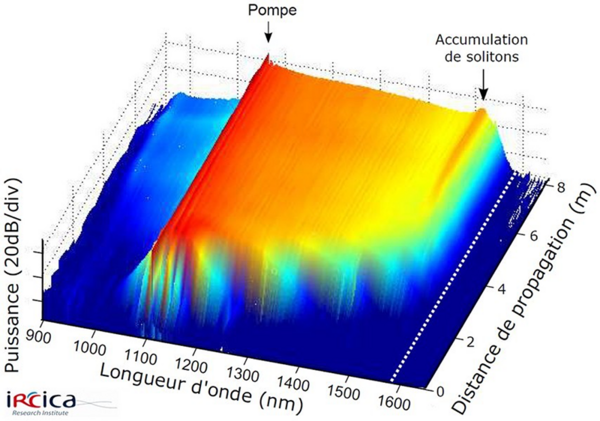
Résultat expérimental : l’étendue spectrale du supercontinuum généré dans la première BIP est limité par la bord de bande (pointillés blancs).
b) Contrôle de l’auto-décalage Raman de solitons
Plus la durée d’un soliton devient faible plus celui-ci devient sensible à l’effet Raman qui cause son décalage vers les hautes longueurs d’onde. Cet effet est nommé : auto-décalage Raman de soliton. Le taux d’auto-décalage d’un soliton dépend de sa durée mais aussi des propriétés linéaires et non-linéaires de la fibre.
Afin d’aller encore plus loin dans le contrôle des solitons temporels, nous avons proposé un nouveau type de fibres optiques – dites fibres topographiques – dans lesquelles les propriétés dispersives et non-linéaires évoluent simultanément et de façon contrôlée en fonction de la longueur de fibre. Nous avons implémenté un algorithme inverse permettant de déterminer le profil longitudinal de fibre optimal pour obtenir une trajectoire spectro-temporelle choisie pour le solitons. Nos expériences ont permis de valider ce concept dans des fibres topographiques fabriquées au sein de la centrale technologique [3].
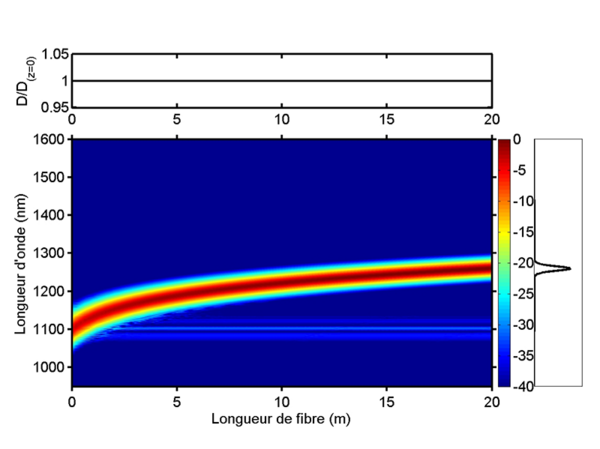
Auto-décalage Raman typique dans une fibre optique uniforme, le décalage est important en début de fibre puis ralentit au cours de la propagation.
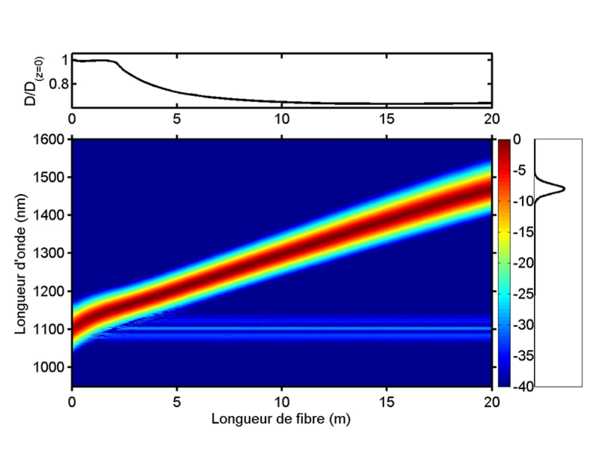
Auto-décalage Raman dans une fibre effilée conçue pour provoquer un auto-décalage important et linéaire en z.
c) Contrôle des Akhmediev breathers et des ondes scélérates optiques
Les Breathers d’Akhmediev sont des solutions analytiques de l’équation de Schrödinger non-linéaire. Leur principal intérêt réside dans l’analogie qui les relie aux vagues scélérates océaniques. Les fibres optiques constituent donc un bon milieu pour l’étude de ces phénomènes extrêmes.
Expérimentalement, ce type de solution peut être excité en propageant dans une fibre optique un champ continu légèrement modulé. Lors de la propagation, cette modulation va croître exponentiellement jusqu’à donner un train d’impulsions courtes. Ensuite, cette croissance va s’inverser et le champ propagé revient à son état initial. Ce processus de croissance-retour se reproduit périodiquement dans la fibre exhibant ce que l’on nomme une récurrence de Fermi-Pasta-Ulam.
En appliquant un saut brusque dans la topographie de la fibre, on peut par exemple altérer cette récurrence et stabiliser le breather à son amplitude maximale.
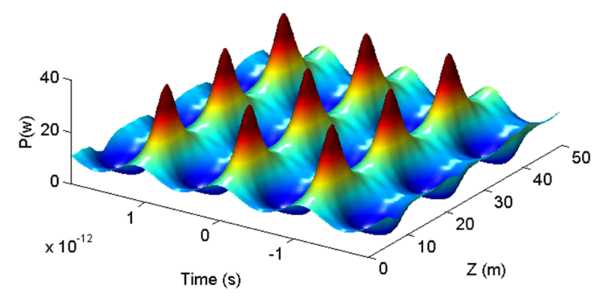
Cycles de croissance-retour résultant d’une excitation non-idéale d’un breather d’Akhmediev dans une fibre uniforme.
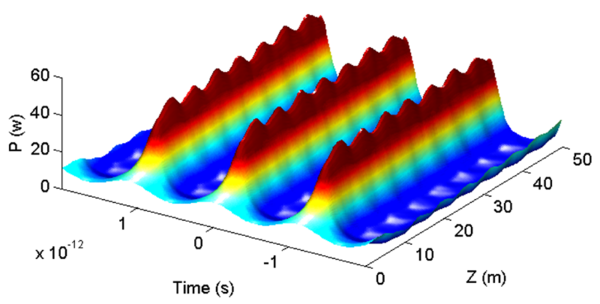
Stabilisation de la forme du breather à son amplitude maximale dans une fibre optique topographique.
