3) Instabilités dans les pièges magnéto-optiques
a) Contexte
Contexte
Les nuages d’atomes froids obtenus à l’aide de pièges magnéto-optiques (PMO) présentent des instabilités spatio-temporelles (variations de la forme et de la position du nuage).
Dispositif expérimental
Pour piéger les atomes de césium contenus dans la cellule, on utilise trois faisceaux perpendiculaires entre eux (Fig. 1). Chacun des faisceaux est réfléchi par un miroir de façon à ce que chaque bras soit constitué de deux faisceaux contra-propageants, l’un polarisé s+ et l ’autre s-.
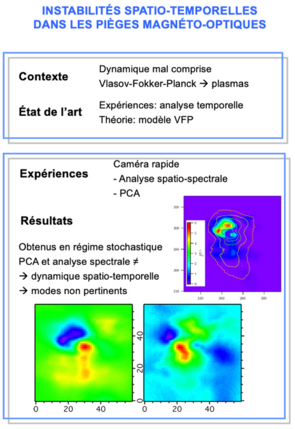
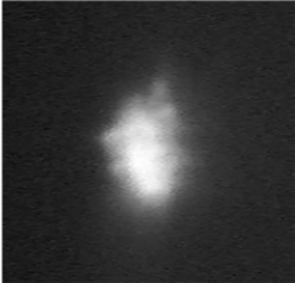
Les instabilités
Les instabilités se traduisent par des variations spatio-temporelles de la forme et de la position du nuage d’atomes froids, ainsi que du nombre d’atomes dans le nuage. On les observe facilement à l’aide d’une caméra CCD enregistrant la fluorescence des atomes dans le nuage. L'animation à droite répète en continu une petite séquence d'une seconde en temps réel.
b) Premières expériences
On réduit le problème spatio-temporel à un système purement temporel en choisissant comme variables dynamiques la position z du centre de masse du nuage et sa population totale n.
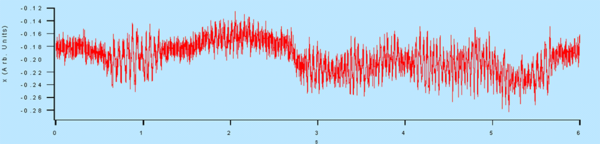
Exemple de comportement de z.
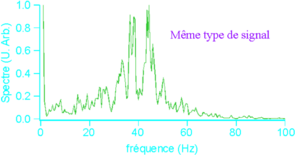
Les instabilités apparaissent dans une région limitée de l’espace des paramètres. La dynamique se fait sur deux composantes de nature et d’échelle de temps différentes. La composante basse fréquence, présente sur les deux variables, est stochastique. Le mouvement correspondant se fait essentiellement sur la première bissectrice des faisceaux aller. La composante « haute » fréquence n’existe que sur la position, et son spectre montre un maximum bien marqué.
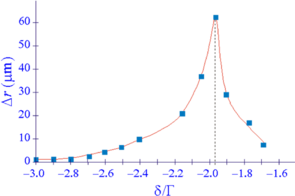
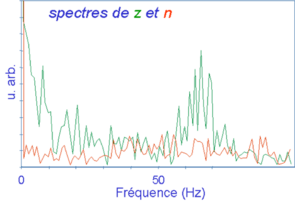
Toutes les méthodes d’analyse échouent à démontrer le déterminisme de ces instabilités. Nous en concluons donc qu'elles sont d'origine stochastique.
c) Base des modèles
L’objectif est de construire le modèle le plus simple possible, permettant de rendre compte des propriétés des instabilités observées dans les expériences et de déterminer les mécanismes à l’origine de ces instabilités. On construit donc un modèle 1D prenant explicitement en compte l’effet d’ombre lié au déséquilibre des faisceaux aller et retour.
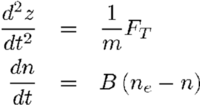
Les équations de base
Pour z, l'équation du mouvement est déterminée par la force totale exercée sur le nuage. Pour n, l'équation tient compte des pertes.
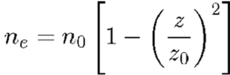
L'équation de la population
Pour tenir compte de la dépendance spatiale des pertes induites dans la population du piège (liée par exemple au profil d’intensité transverse des faisceaux du piège), on introduit une dépendance de ne en z. Bien que cette dépendance soit nécessaire pour l’apparition des instabilités, sa forme est peu critique.
d) Modèle global
Dans ce modèle, on ne considère que l’absorption globale du faisceau par le nuage : I2 = I1 e-a < I1. Les équations s’écrivent :
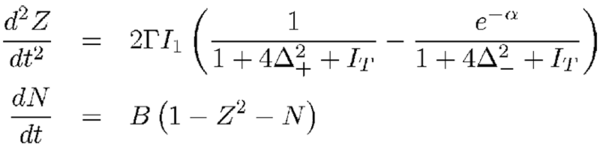
Les solutions stationnaires forment un pli dans l’espace des phases.

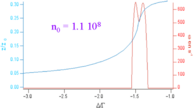
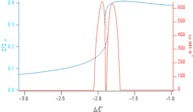
Dans les conditions des premières expériences, les solutions stationnaires sont uniques et stables. On construit donc un modèle stochastique en rajoutant du bruit sur n0 ou I1. On reproduit alors très bien les observations expérimentales.
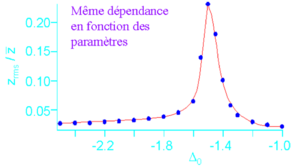
e) Modèle en propagation
Dans ce modèle, on écrit FT en fonction de I1, I2 et I3: equations en propagation
À partir des équations de la matrice densité, on écrit les équations de propagation des faisceaux aller et retour. On introduit ensuite une densité atomique constante r qui permet de déduire la relation entre I1, I2 et I3, ainsi que la taille S du piège.
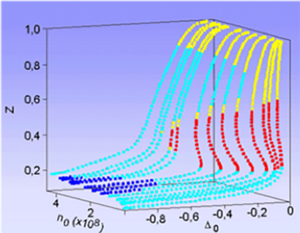
Dans l’espace des phases, la forme des solutions stationnaires est similaire à celle obtenue avec le modèle global, ainsi qu'on peut le voir sur la figure 11, où les couleurs codent la nature du point fixe: noeud stable, foyer stable, noeud selle (instable) ou foyer selle (instable).
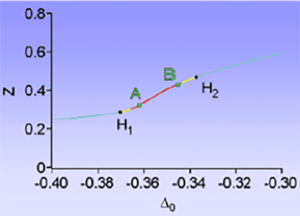
Au voisinage de la zone bistable, il existe une zone instable apparaissant à travers deux bifurcations de Hopf (H1 et H2).
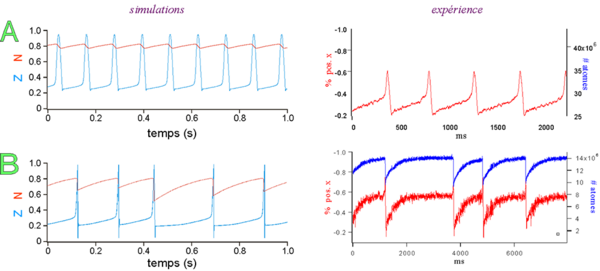
f) Instabilités déterministes
Dans les zones instables, on obtient des instabilités périodiques (A) au voisinage de la bifurcation de Hopf la plus éloignée de la résonance, et du chaos (B) quand on se rapproche de la résonance :